Shearing interferometer
The shearing interferometer is an extremely simple means to observe interference and to use this phenomenon to test the collimation of light beams, especially from laser sources which have a coherence length which is usually a lot longer than the thickness of the shear plate (see graphics) so that the basic condition for interference is fulfilled.
Function
The testing device consists of a high quality optical glass (like BK-7) with extremely flat optical surfaces and usually having a slight angle between them. When a plane wave is incident at an angle of 45° (which gives maximum sensitivity) it is reflected two times. The two reflections are laterally separated due to the finite thickness of the plate and by the wedge. This separation is referred to as the shear and has given the instrument its name. The shear can also be produced by gratings, see External Links below.
Parallel-sided shear plates are sometimes used but the interpretation of the interference fringes of wedged plates is relatively easy and straightforward. Those wedged shear plates produce a graded path difference between the front and back surface reflections. As a consequence, a parallel beam of light produces a linear fringe pattern within the overlap.
With a plane wavefront incident, the overlap of the two reflected beams shows interference fringes with a spacing of 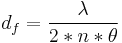 , with
, with  being the wavelength of the beam, n being the refractive index and
being the wavelength of the beam, n being the refractive index and  the wedge angle. The fringes are equally spaced and will be exactly perpendicular to the wedge orientation and parallel to a usually present wire cursor aligned along the beam axis in the shearing interferometer. The orientation of the fringes varies (i.e. they are tilted on the screen) when the beam is not perfectly collimated but diverging or converging. In the latter case of a noncollimated beam (thus having a curved wavefront) is incident on a wedged shear plate the path difference between the two reflected wavefronts is increased or decreased from the case of perfect collimation, depending on the sign of the curvature. The pattern is then rotated and the beam's wavefront radius of curvature
the wedge angle. The fringes are equally spaced and will be exactly perpendicular to the wedge orientation and parallel to a usually present wire cursor aligned along the beam axis in the shearing interferometer. The orientation of the fringes varies (i.e. they are tilted on the screen) when the beam is not perfectly collimated but diverging or converging. In the latter case of a noncollimated beam (thus having a curved wavefront) is incident on a wedged shear plate the path difference between the two reflected wavefronts is increased or decreased from the case of perfect collimation, depending on the sign of the curvature. The pattern is then rotated and the beam's wavefront radius of curvature  can be calculated:
can be calculated: 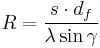 , with
, with  the shear distance,
the shear distance, 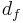 the fringe distance,
the fringe distance,  the wavelength and
the wavelength and  the angular deviation of the fringe alignment from that of perfect collimation.
the angular deviation of the fringe alignment from that of perfect collimation.